
“The most beautiful thing one can experience is the mysterious. It is the source of all true Art and Science” – Albert Einstein |
|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Part of GEIST's magic is its alluring board. Unlike many other board games which use the board just to keep track of players' progress in the game, GEIST truly involves the board. In GEIST, players must use the relationships between the numbers on the board to generate their movements and the board itself is a tool in your arsenal for play.
The GEIST board is based on a fabulous triangle called the Pascal's Triangle. The wonder of this mathematical beauty has never ceased to fascinate since its discovery in ancient times. It is not only known for its extraordinary internal patterns and relationships, but also for its applications in several fields of mathematics, and now in GEIST! For those already familiar with the Pascal's Triangle, I hope you will take delight in this new concept for a board game based on the fascinating triangle.
In GEIST, the first seven rows of the triangle are repeated 4 times around the board, in a harmonious, symmetrical arrangement, and encircled by 4 unmarked squares on the outer corners. An original and artful game board was thus created and along with GEIST's clever rules of movement, gives you a most thrilling and challenging game!
For the curious minds, read on to learn more about this mathematical marvel called the Pascal's Triangle! While the information conveyed below is not needed to play GEIST, it will reveal the secrets behind the triangle |
What is the Pascal's Triangle? |
Mysteries of the Pascal's Triangle |
What is Pascal's Triangle used for? |
 |
Pascal's Triangle has been compared to "either as a gold mine or as an iceberg - the former because the riches are there, but some ingenious labor is often needed; the latter because we shall perhaps never see more than a small percentage of the mass."
Pascal's Triangle is named after 17th century French mathematician and philosopher, Blaise Pascal (1623-1662), following his completion of the Treatise on the Arithmetical Triangle where he developed many of the triangle's properties and applications. Although, the triangle came to be known as Pascal's Triangle, Pascal was not the first to discover this triangle. It was discovered independently by other mathematicians long before his time. 10th century Indian mathematicians and the great 11 th century mathematician, Omar Khayyam, who lived in what is modern-day Iran, mentioned this triangle in their writings. A depiction of the triangle was also featured prominently in the treatise "The Precious Mirror of the Four Elements" by the Chinese mathematician Chu Shih Chieh in 1303. In this treatise, Chu Shih Chieh indicated the use of the triangle in providing coefficients for the binomial expansion of ( a+b)n .
Pascal's work on the triangle stemmed from a gambling problem. Given the penchant for gambling from various cultures throughout times, one would expect the mathematics of chance to be one of the earliest to have been formulated. Surprisingly, it wasn't until 1654, when Pascal was approached by a French nobleman, Chevalier de Méré, with questions concerning a popular dice game, that an accurate mathematical field of probability was developed. Intrigued by the Chevalier's questions, Pascal shared them with Pierre de Fermat, another fellow mathematician. This led to an exchange of letters, and Pascal began to investigate the chances of getting different values for rolls of the dice. His discussions with Fermat are considered to have laid the foundation for the theory of probability, and Pascal's Triangle was the result.
Pascal's Triangle is not a geometrical triangle but a triangle of numbers. It is a triangle made up of staggered rows of numbers, more specifically, rows of integers, with a "1" on top and down the sides. The first eight rows of the triangle look like this: |
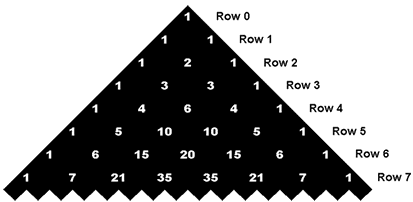 |
| Notice that every number in the interior of the triangle is the sum of the two numbers directly above it. The rows of the triangle can go on indefinitely.
|
 |
 |
To fully appreciate this mathematical marvel, one should look deeper into its rows and diagonals. Some of its greatest mysteries lie in the many interesting patterns that emerge.
First, notice that the numbers within the triangle are symmetric. In other words, if we were to fold the triangle across its altitude the numbers on either side of the fold match exactly.
Sum of the Rows – One of the triangle's first mysteries is called the “Sum of the Rows”.
When the numbers in any row are summed up, the sum equals 2n , where n is the number of the row: |
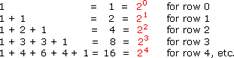 |
| Powers of 11 – Another interesting mystery can be found within the triangle: the powers of 11 can be extracted if you read across the rows and interpret the digits as a place value system: |
 |
However, starting in row 5, it's harder to see the pattern. That's because a two-digit number like the number 10 can not occupy a single place. You can think of row 5 in this way:
1(105) + 5(104) + 10(103) + 10(102) + 5(101) + 1(100 )
= 100000+50000+10000+1000+50+1
= 161051
Below is another representation that can help you understand the relationship between Pascal's Triangle and the powers of 11:
Since 11 = (10+1), let x = 10, then:
110 = 1
111 = (x+1)1 = 1 x +1 = 11
112 = (x+1)2 = 1 x2 + 2 x +1 = 100+20+1 = 121
113 = (x+1)3 = 1 x3 + 3 x2 + 3 x +1 = 1000+300+30+1 = 1331
114 = (x+1)4 = 1 x4 + 4 x3 + 6 x2 + 4 x +1 = ……….. = 14641
115 = (x+1)5 = 1 x5 + 5 x4 + 10 x3 + 10 x2 + 5 x + 1 ……….. = 161051
.............
If you just look at the coefficients (in red) of the representation above, you'll see Pascal's Triangle!
Prime Numbers – Yet, another interesting pattern can be found in the triangle that relates to prime numbers. If n is a prime number, then all the middle terms (all terms except the two end terms) of the nth row are divisible by n. In other words, for any prime numbered row, all the numbers in that row (excluding the 1's) are divisible by the prime. For example, in the 5th row, 5 and 10 are all divisible by 5.
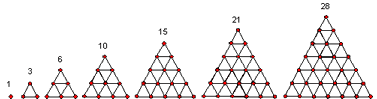
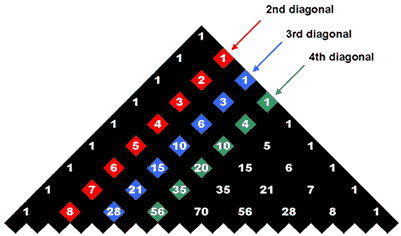
Triangular Numbers and Tetrahedral Numbers – More fascinating mysteries of the triangle can be discovered by examining its diagonals. The 2nd diagonal is the sequence of counting numbers (1, 2, 3, 4, . . .). The 3rd diagonal is the sequence of triangular numbers (1, 3, 6, 10, . . .). A triangular number is a figurate number, that is, a number that can be represented by a regular geometric arrangement of equally spaced points. They can also be thought of as the numbers of dots required to build a triangle: |
 |
| Another sequence that can be found in the Pascal Triangle is the set of tetrahedral numbers, or the sums of the triangular numbers (1, 4, 10, 20, . . .) located in the 4th diagonal. |
 |
| The Fibonacci Numbers – The Fibonacci numbers are a bit harder to find within the triangle. The famous Fibonacci's sequence is as follows: 1, 1, 2, 3, 5, 8, 13 . . . It begins with two 1's, and then all other numbers are generated by summing the two previous numbers in the sequence. To find the Fibonacci numbers in the triangle, you need to go up at an angle and look for 1, 1, 1+1, 1+2, 1+3+1, 1+4+3, 1+5+6+1,....loccated on each of the drawn-in diagonals below. |
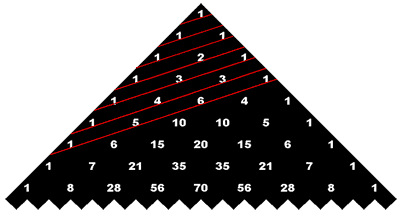 |
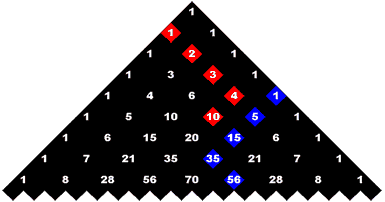
Hockey Stick – My favorite pattern found within Pascal's Triangle is the one called the "Hockey Stick" Pattern. Try to do this: select a diagonal of numbers of any length starting with any of the 1's down the sides of the triangle and ending on any number inside the triangle. The sum of the numbers of that diagonal is equal to the number right below the last number of the diagonal, but which is not on the diagonal. Can you see the hockey stick in the diagram below?
Let's try the following examples of the Hockey Stick Pattern:
1 + 2 + 3 + 4 = 10
1 + 5 + 15 + 35 = 56 |
|
 |
 |
Pascal's Triangle is not only fascinating because of all of its hidden patterns, but also because of its wide expanse of applications to many areas of mathematics, particularly in Probability and Algebra. Its known applications in mathematics also extend to calculus, trigonometry, plane geometry, and solid geometry.
Probability/Combinatorics
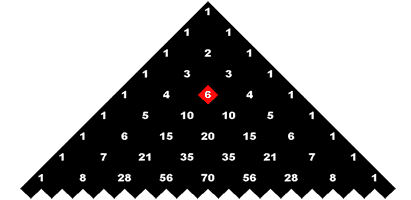
Pascal's Triangle can be used to find “Combinations”. Let's suppose you want to know how many different duets can be formed from a group of 4 instrumentalists. This problem basically amounts to the question "how many different ways can you pick 2 instrumentalists when there are 4 people to choose from?"
The answer is in the triangle! It's the number in the 2nd place of the 4th row, i.e. 6 (entries in Pascal's Triangle are usually given a row number and a place in that row, beginning with row zero and place zero). So there are 6 different ways to choose 2 people from a set of 4. |
 |
Therefore, Pascal's Triangle is a very useful tool in finding, the number of subsets of k elements that can be formed from a set of n distinct elements!
Algebra
In Algebra, we can use Pascal's Triangle to figure out what a binomial raised to a power will be. Let's take the binomial (X+ Y) and raise it to the power 5. Raising (X + Y) to the power 5 can be thought of as repeated multiplication as follows:
(X + Y) 5 = (X + Y) (X + Y) (X + Y) (X + Y) (X + Y)
To expand this expression, we would have to use the distributive property over and over again. This would be very tedious, but, once again, thanks to Pascal's Triangle, we can perform this quickly. Write out in order all the power combinations - 5 X's and no Y's, 4 X's and 1 Y, 3 X's and 2 Y's, etc., up to no X's, then use the numbers in row 5 of the triangle as coefficients:
--> (X + Y) 5 = 1 X 5 + 5 X 4 Y + 10 X 3 Y 2 + 10 X 2 Y 3 + 5 X Y 4 + 1 Y 5
Let's write out the binomial (X+ Y) raised to the powers 0,1,2,3,4,5…: |
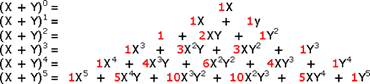 |
| Look at the coefficients of the results above and you'll see Pascal's Triangle! The numbers in each row of the triangle are precisely the same numbers that are the coefficients of binomial expansions. Because of this connection, the entries in Pascal's Triangle are called the binomial coefficients. |
 |
 |
I hope this short account has conveyed some of the most intriguing and interesting attributes known about Pascal's Triangle. Still, it seems we have only scratched the surface. I encourage you to seek out new patterns and uncover more of its secrets. GEIST, like the triangle, is also full of mysteries and surprises. The more you play it, the more you'll uncover its hidden strategies.
Rose |
 |
|

|
 |
 |
 |
 |
 |
 |
 |
 |
 |
|
|